Quarter Exams will be curved (top score is 100%) and represents 20% of your grade (10% each). The exam will have some multiple choice and response questions ("inspired" by the 2025 FRQ's).
| No Calculator | Calculator Active | Total | |
|---|---|---|---|
| Multiple Choice | 9 questions-18 points | 5 questions-9 points | 14 questions-27 points (50%) |
| Free Response | 2 questions-18 points | 1 question-9 points | 3 questions-27 points (50%) |
| Total | 11 questions-36 points (2/3) | 6 questions-18 points (1/3) | 17 questions - 54 raw points |
| Recommended Time | 60 min | 30 min | 90 min |
The review packets and solutions (BC MC 2- BC MC 5 and BC FR 2-BC FR 5) are at Portals Under the "BC Practice Exam" Topic as well as AB Questions (MC 1-8, FR 1-8) are at the SFHS Portal in the "AB Practice Exams" Topic (look for the Homer Simpson picture with "The End is Near" sign). Additional practice can be found on DeltaMath.com, and myAp.collegeboard.com (Including Daily Videos on all Topics). Most questions should remind you of all the AP practice questions we have been doing all quarter. The review packets (MC1-MC5, FR1-5) are at hw.mathorama.com and the solutions are on plus portal. Additional practice can be found on DeltaMath.com, and myAp.collegeboard.com (Including Daily Videos on all Topics).
The questions on the exam do not require difficult calculations, but an understanding of the concepts. There is more thought than brute force necessary to come up with the correct solutions.
Students are expected to show enough of their work for Readers to follow their line of reasoning. To obtain full credit for the solution to a free-response problem, students must communicate their methods and conclusions clearly. Answers should show enough work so that the reasoning process can be followed throughout the solution. This is particularly important for assessing partial credit. Students may also be asked to use complete sentences to explain their methods or the reasonableness of their answers, or to interpret their results.For results obtained using the calculator capabilities of plotting, finding zeros, finding the numerical derivative or integral, students are required to write the setup (e.g., the equation being solved, or the derivative or definite integral being evaluated) that leads to the solution, along with the result produced by the calculator.
For example, if the student is asked to find the area of a region, the student is expected to show a definite integral (i.e., the setup) and the answer. The student need not compute the antiderivative; the calculator may be used to calculate the value of the definite integral without further explanation.
For solutions obtained using the calculator capabilities, students must also show the mathematical steps that lead to the answer; a calculator result is not sufficient. For example, if the student is asked to find a relative minimum value of a function, the student is expected to use calculus and show the mathematical steps that lead to the answer. It is not sufficient to graph the function or use a built-in minimum folder.
When a student is asked to justify an answer, the justification must include mathematical reasons, not merely calculator results. Functions, graphs, tables, or other objects that are used in a justification should be clearly identified.
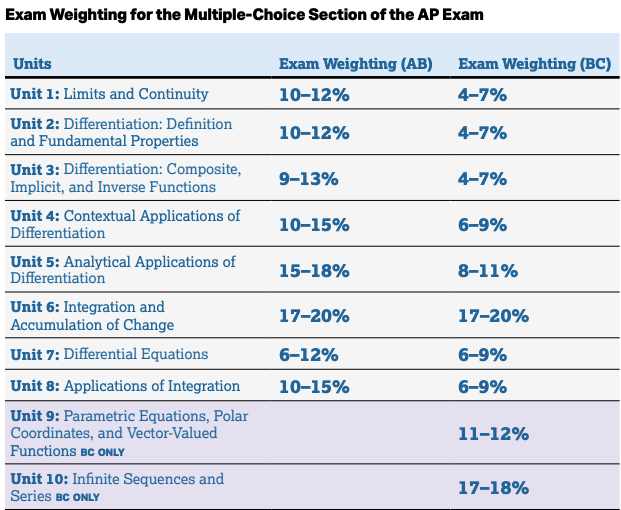
Our Sem 2 Exam is only 90 minutes, but will include a few Financial Math questions from the time after the exam, and all ten units of the AP Calculus Course and Exam Description (CED):

The College Board (that administers the AP exams) has this helpful passage about what should be included in a free response question:
Students are expected to show enough of their work for Readers to follow their line of reasoning. To obtain full credit for the solution to a free-response problem, students must communicate their methods and conclusions clearly. Answers should show enough work so that the reasoning process can be followed throughout the solution. This is particularly important for assessing partial credit. Students may also be asked to use complete sentences to explain their methods or the reasonableness of their answers, or to interpret their results.For results obtained using the calculator capabilities of plotting, finding zeros, finding the numerical derivative or integral, students are required to write the setup (e.g., the equation being solved, or the derivative or definite integral being evaluated) that leads to the solution, along with the result produced by the calculator.
For example, if the student is asked to find the area of a region, the student is expected to show a definite integral (i.e., the setup) and the answer. The student need not compute the antiderivative; the calculator may be used to calculate the value of the definite integral without further explanation.
For solutions obtained using the calculator capabilities, students must also show the mathematical steps that lead to the answer; a calculator result is not sufficient. For example, if the student is asked to find a relative minimum value of a function, the student is expected to use calculus and show the mathematical steps that lead to the answer. It is not sufficient to graph the function or use a built-in minimum folder.
When a student is asked to justify an answer, the justification must include mathematical reasons, not merely calculator results. Functions, graphs, tables, or other objects that are used in a justification should be clearly identified.
Here is a check list of the topics:
Bring a calculator, a number 2 pencil and good eraser as all scantron responses are graded according to what the machine interprets (this is to prepare you to the cruel reality of how it is with AP Exams and other standardized tests)
The exam is worth 20%, and will be curved.
Remember to a good night's rest, and eat a healthy breakfast!
Good Luck!