Stereoscopic Dots 3D
Drag to rotate around the vertical axis
You need Red-Cyan glasses of course
The Rotation & Perspective Formulas
|
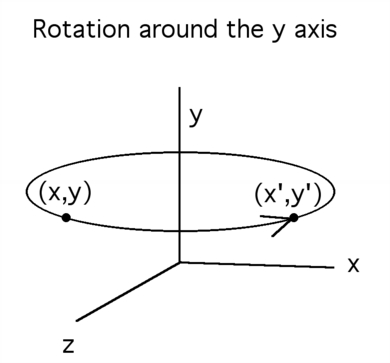
As the point revolves around
the y axis, it follows the path
of a circle, always at the same
height(y) and distance (the radius
of the circle) from the turning point
(the y axis).
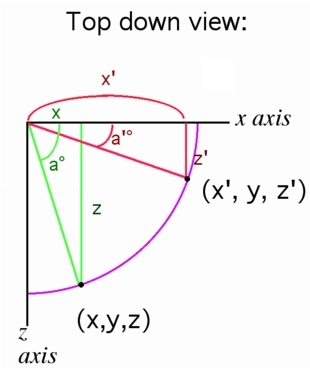
A green right triangle can be formed from the turning point, the original location (x,y,z) and the axes.
Since
Solving the equation for z,
Therefore, to get the new location (x', y, z')
we can see the red triangle can be formed,
and
By similar means the new x' will be
Since cos a° = adjacent/hypotenuse
and in the green triangle so that |
|
What's next?
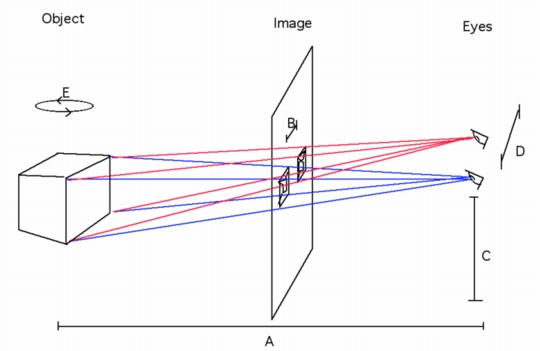
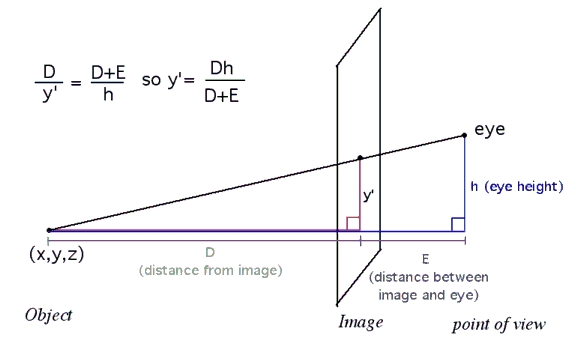
The wonderful brain you have helps you to see two images as one, with an intuitive sense of the geometry of two view points. The closer the object the more different the view on the left is from the view on the right. Another explanation is here3D Anaglyphs Links
- See the shuttle's 3D Map of St. Francis High (and JPL) taken in February 2000.
- Bonneville, Mars 3/17/04
- Bonneville 3/12/04
- Adirondack Pre RAT Drill 2/12/04
- Adirondack post RAT drill 2/12/04
- Mars Berries on the ground 2/12/04
- More Mars Berries 2/12/04
- Even More Berries 2/12/04
- Traversing Martian Terrain 2/6/04
- Opportunity Stretches Out 2/2/04
- JPL or 3DGlasses.com or Rainbow Sympony or 3D Expo!
Secondly, you can see how the brain will even try to make two views from one in Single Image Random Dot Stereograms (SIRDS).
Finally, the computer can be fed new shapes, by describing the shape in terms of 3-D co-ordinates (x, y, z). See how you can make your own 3-D shapes here.
Other information
The java source that made this demonstration is here.