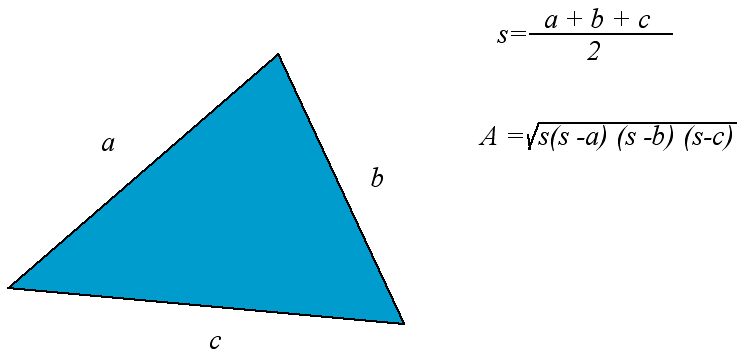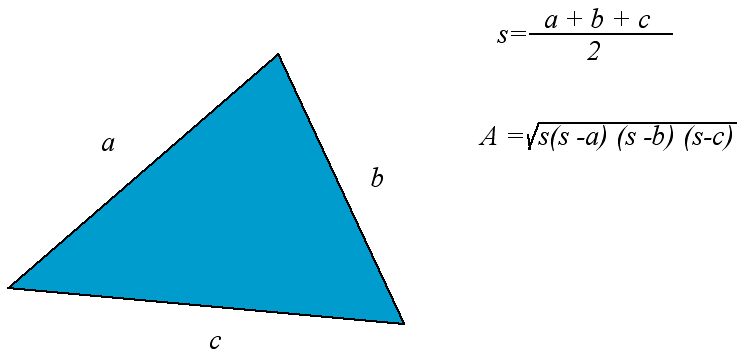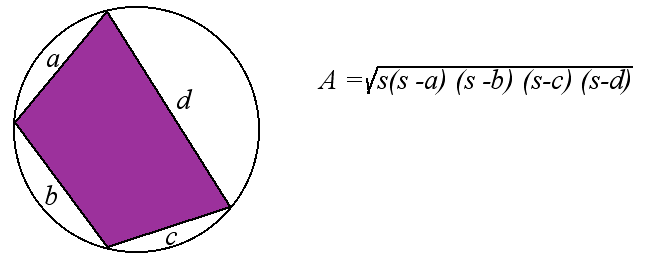Heron's Formula

Heron, a Mathematician from the hight of Alexandrian culture (over 2000 years ago), derived this formula. Normally, the area of a triangle can be computed by taking half the base times the altitude. The problem is that it may not be convenient to compute the altitude of a triangle. Heron found a way to compute the area simply from knowing the lengths of each side.

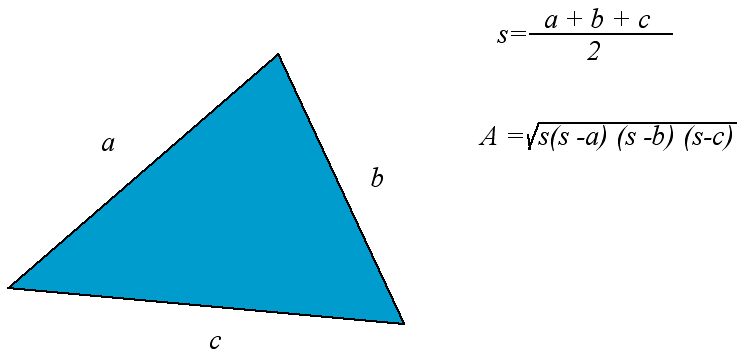The formula is the square root of the product of half the perimeter with the difference between each side and half the perimeter. To compute this by hand, first find the "semiperimeter" s by adding the sides and dividing by 2. Then multiply s * (s-a) * (s-b) * (s-c). Finally, take the square root of this product.

Challenge 1

Try to compute the area of triangles with the following lengths:

9,10,11
5,7,8
6,11,13
15,16,17
6.3,7.2,10.1
68,77,105
5.5,6.5,10
12,18,27
3,4,5
6,6,6
13,13,10
29,29,42

Challenge 2

It turns out that Heron's formula has a weakness. Try computing the area of a triangle with sides that measure 47, 38, and 85. Why would this cause a problem?

Challenge 3

It turns out that Heron's formula can be extended to compute the area of any quadrilateral, so long as it can be inscribed in a circle. Try to modify the script of this web page to include a forth side d so it can compute the area of a quadrilateral with sides 10, 10, 10, and 20.

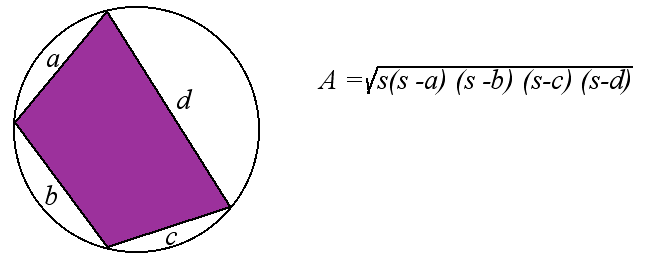
The javascript that makes this page work was written by Fr. Chris. If you have any problems, comments or sugestions, please e-mail me at cct@ktb.net