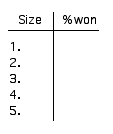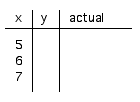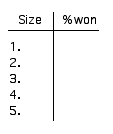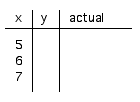Disk Game
The game is played by tossing a disk on tiles 9 inches square.
To win, you must toss the disc so it lands on a crack.
If the winner gets $2, what would be a fair price to
play the game? It depends more on the size of the
disk than the skill of the player.
Answer the questions on page 178.
Challenge Questions:
- Using 9 inch tiles, find the win/loss proportion for 5 different sizes of disk (all under 4 inches), and
record the size and percentage of wins.
- Make a scatterplot of your data.
- Find the linear regression line. What is the equation?
- Use the equation to predict the percentage of wins for 5, 6, and 7 inch disks.
- Use the simulation to see if the data match your predictions.
- Did they match?
- Try a non-linear model (make a linear regresson line with the log(% of wins) vs. size rather than
% of wins vs. size like we did last week in class... see pages 180-181, 185.
- What is the the equation for the logarythmic model (see p. 185)?
- Use this equation to predict 5, 6, and 7 inch disks. Is it a better estimate than the
first equation you used?
- If the disk is 3" and the tile is 9" what would be a
fair jackpot if it costs $1 to play?
- What would be a fair size disk (50% wins) for 4 inch tiles?
- What would be a fair size disk (50% wins) for 6 inch tiles?
- What would be a fair size disk (50% wins) for 9 inch tiles?
- What would be a fair size disk (50% wins) for 12 inch tiles?
- What would be a fair size disk (50% wins) for 16 inch tiles?
- Is there a pattern? Make a scatterplot/regression line to
predict the fair size disk for a 18, 20, and 24 inch grid.
This simulation was written by Fr. Chris Thiel, OFMCap
(cthiel@sfhs.net).
If you want to start learning how to program, take a look at the Java source code.