Chapter 8
<< Chapter 7 | HomeworkTrailIndex | Chapter 9 >>
Designing Classes
JUnitTesting with BlueJ tutorial
Demos
Review Exercises
R8.1
Users place coins in a vending machine and select a product by pushing a button. If the inserted coins are sufficient to cover the purchase price of the product, the product is dispensed and change is given. Otherwise, the inserted coins are returned to the user.
What classes should you use to implement it?
R 8.6
Suppose a vending machine contains products, and users place coins into the vending machine to purchase products.
Draw a UML diagram showing the dependencies between the classes VendingMachine, Coin, and Product
R 8.9
Classify (Accessor or Mutator) the methods of the class Scanner that are used in this book as accessors and mutators.
boolean hasNext() boolean hasNextDouble() boolean hasNextInt() boolean hasNextLine() String next() double nextDouble() int nextInt() String nextLine()
Programming Exercises
For 8 points do P8.5, P8.6, P8.10, P8.11. For 9 points, add P8.7. For 10 Points add P8.8. For 11 out of 10, add A JUnit Class.
8.5 Write static methods
public static double sphereVolume(double r) public static double sphereSurface(double r) public static double cylinderVolume(double r, double h) public static double cylinderSurface(double r, double h) public static double coneVolume(double r, double h) public static double coneSurface(double r, double h)
that compute the volume and surface area of a sphere with radius r, a cylinder with circular base with radius r and height h, and a cone with circular base with radius r and height h. Place them into a class Geometry. Then write a program that prompts the user for the values of r and h, calls the six methods, and prints the results.
Here are some helpful formulas:
{⚠ $V_{sphere}=\frac{4}{3}\pi r^3 $}
{⚠ $A_{sphere}=4\pi r^2$}
{⚠ $V_{cone}=\frac{\pi}{3} h r^2$}
{⚠ $A_{cone}=\pi r^2+\pi r \sqrt{r^2+h^2}$}
{⚠ $V_{cylinder}=\pi h r^2$}
{⚠ $A_{cylinder}=2\pi r^2+2\pi r h$}
Here is a screen capture of me writing the first method:
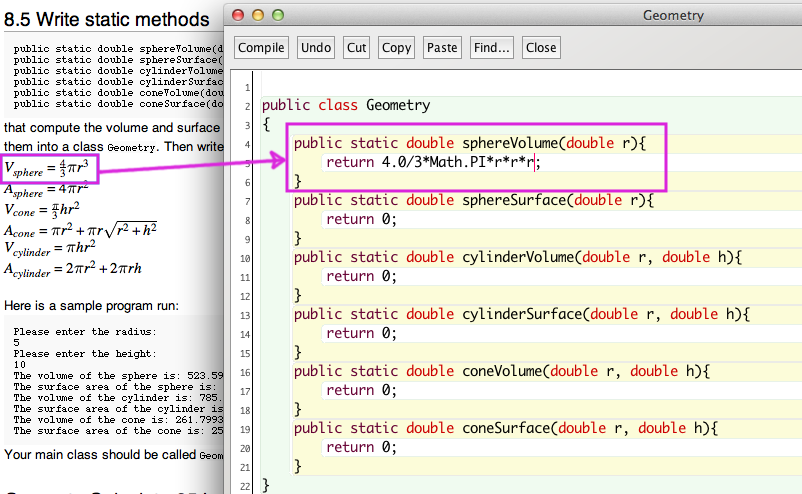
Before you work on your main method of GeometryCalculator85.java, you may wish to try my JUnit for testing your Geometry class
GeometryTest.java
import static org.junit.Assert.*;
import org.junit.After;
import org.junit.Before;
import org.junit.Test;
/**
* The test class GeometryTest.
*
* @author (your name)
* @version (a version number or a date)
*/
public class GeometryTest
{
/**
* Default constructor for test class GeometryTest
*/
public GeometryTest()
{
}
/**
* Sets up the test fixture.
*
* Called before every test case method.
*/
@Before
public void setUp()
{
}
/**
* Tears down the test fixture.
*
* Called after every test case method.
*/
@After
public void tearDown()
{
}
@Test
public void SphereVolumeTest()
{
assertEquals(0.0, Geometry.sphereVolume(0.0), 0.0001);
assertEquals(4.18879, Geometry.sphereVolume(1.0), 0.0001);
assertEquals(1098.066219, Geometry.sphereVolume(6.4), 0.0001);
}
@Test
public void SphereSurfaceTest()
{
assertEquals(0, Geometry.sphereSurface(0), 0.001);
assertEquals(12.5663706, Geometry.sphereSurface(1.0), 0.001);
assertEquals(314.1592653589793, Geometry.sphereSurface(5.0), 0.001);
}
@Test
public void CylinderVolumeTest()
{
assertEquals(9.4247779, Geometry.cylinderVolume(1.0, 3.0), 0.001);
assertEquals(785.3981633974483, Geometry.cylinderVolume(5.0, 10.0), 0.001);
}
@Test
public void CylinderSurfaceTest()
{
assertEquals(471.23889803846896, Geometry.cylinderSurface(5.0, 10.0), 0.0001);
}
@Test
public void ConeVolumeTest()
{
assertEquals(261.799387, Geometry.coneVolume(5.0, 10.0), 0.1);
}
@Test
public void ConeSurfaceTest()
{
assertEquals(254.1601846, Geometry.coneSurface(5.0, 10.0), 0.0001);
}
}
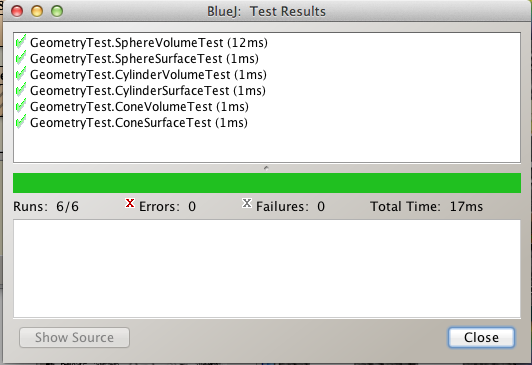
Once you have your static methods passing the JUnit test, complete the GeometryCalculator85 class to test the remaining 4 methods of the Geometry class (To save time, you can borrow the expected values from my JUnit test class above).
GeometryCalculator85.java
import java.util.Scanner;
/**
* GeometryCalculator85 here.
*
* @author Your Name
* @version today's date
*/
public class GeometryCalculator85
{
public static void main(String[] args)
{
System.out.println("The radius: 5.0");
System.out.println("The height: 10.0");
double r=5.0;
double h=10.0;
System.out.print("The area of the cone is: "+Geometry.coneSurface(r,h));
System.out.println("-- Expected 254.160184615763");
System.out.print("The volume of the cone is: "+Geometry.coneVolume(r,h));
System.out.println("-- Expected 261.79938779914943");
// your code here:
}
}
P8.6.
Solve Exercise P8.5 by implementing classes Sphere, Cylinder, and Cone. Which approach is more object-oriented?
/**
* GeometryCalculator85 here.
*
* @author Your Name
* @version today's date here
*/
public class GeometryCalculator86
{
public static void main(String[] args)
{
System.out.println("The radius: 5.0");
System.out.println("The height: 10.0");
double r=5.0;
double h=10.0;
Sphere ball = new Sphere(r);
Cylinder cyl = new Cylinder(r, h);
Cone cone = new Cone(r, h);
System.out.print("The area of this sphere is: "+ball.surface());
System.out.println("-- Expected ???"); // replace the ??? with the correct number
System.out.print("The volume of this sphere is: "+ball.volume());
System.out.println("-- Expected ???"); // replace the ??? with the correct number
System.out.print("The area of this cylinder is: "+cyl.surface());
System.out.println("-- Expected ???"); // replace the ??? with the correct number
System.out.print("The volume of this cylinder is: "+cyl.volume());
System.out.println("-- Expected ???"); // replace the ??? with the correct number
System.out.print("The area of this cone is: "+cone.surface());
System.out.println("-- Expected 254.160184615763");
System.out.print("The volume of this cone is: "+cone.volume());
System.out.println("-- Expected 261.79938779914943");
}
}
Hint for 8.6
Here is the Cone class:
public class Cone
{
// instance variables - replace the example below with your own
private double r,h;
/**
* Constructor for objects of class Cone
*/
public Cone(double radius, double height)
{
// initialise instance variables
this.r=radius;
this.h=height;
}
/**
* @return surface area of this cone
*/
public double surface()
{
return Math.PI*r*r+Math.PI*r*Math.sqrt(r*r+h*h);
}
/**
* @return volume of this cone
*/
public double volume(){
return (Math.PI/3.0)*h*r*r;
}
}
P8.7.
Write methods
public static double perimeter(Ellipse2D.Double e); public static double area(Ellipse2D.Double e);
that compute the area and the perimeter of the ellipse e. Add these methods to a class Geometry. The challenging part of this assignment is to find and implement an accurate formula for the perimeter. To help, use the API to find the width and height. The formulas involve HALF the major axis {⚠ $a$} and HALF the minor axis {⚠ $b$}.
{⚠ $A_{ellipse}\approx \pi a b $}
{⚠ $P_{ellipse} \approx 2\pi \sqrt{\frac{1}{2}(a^2+b^2)} $}
Why does it make sense to use a static method in this case?
Use the following class as your tester class:
import java.awt.geom.Ellipse2D;
/**
This is a tester for the ellipse geometry methods.
*/
public class EllipseTester
{
public static void main(String[] args)
{
Ellipse2D.Double e = new Ellipse2D.Double(100, 100, 200, 100);
System.out.println("Area: " + Geometry.area(e));
System.out.println("Expected: 15707.963267948966");
System.out.println("Perimeter: " + Geometry.perimeter(e));
System.out.println("Expected: 496.7294132898051");
}
}
P8.8.
Write methods
public static double angle(Point2D.Double p, Point2D.Double q) public static double slope(Point2D.Double p, Point2D.Double q)
that compute the angle between the x-axis and the line joining two points, measured in degrees, and the slope of that line. Add the methods to the class Geometry. Supply suitable preconditions (think about what input would cause an error). Why does it make sense to use a static method in this case?
Use the following class as your tester class:
import java.awt.geom.Point2D;
/**
This program tests the methods to compute the slope and
angle of a line.
*/
public class LineTester
{
public static void main(String[] args)
{
Point2D.Double p = new Point2D.Double(-1, -1);
Point2D.Double q = new Point2D.Double(3, 0);
System.out.println("Slope: " + Geometry.slope(p, q));
System.out.println("Expected: 0.25");
Point2D.Double r = new Point2D.Double(0, 0);
System.out.println("Angle: " + Geometry.angle(p, r));
System.out.println("Expected: -135");
}
}
Hint: use Math.atan2
P8.10.
Write a method
public static int readInt(
Scanner in, String prompt, String error, int min, int max)
that displays the prompt string, reads an integer, and tests whether it is between the minimum and maximum. If not, print an error message and repeat reading the input. Add the method to a class Input.
Use the following class as your main class:
import java. util.Scanner;
/**
This program prints how old you'll be next year.
*/
public class AgePrinter
{
public static void main(String[] args)
{
Scanner in = new Scanner(System.in);
int age = Input.readInt(in, "Please enter your age",
"Illegal Input--try again", 1, 150);
System.out.println("Next year, you'll be " + (age + 1));
}
}
P8.11.
Consider the following algorithm for computing {⚠ $x^n$} for an integer {⚠ $n$}. If {⚠ $n < 0$}, {⚠ $x^n$} is {⚠ $\frac{1}{x^{-n}}$}. If {⚠ $n$} is positive and even, then {⚠ $x^n = (x^{n/2})^2$}. If {⚠ $n$} is positive and odd, then {⚠ $x^n = x \cdot x^{n-1}$} . Implement a static method double intPower(double x, int n) that uses this algorithm. Add it to a class called Numeric.
Use the following class as your tester class:
/**
This is a test driver for the intPower method.
*/
public class PowerTester
{
public static void main(String[] args)
{
System.out.println(Numeric.intPower(0.1, 12));
System.out.println("Expected: " + 1E-12);
System.out.println(Numeric.intPower(2, 10));
System.out.println("Expected: 1024");
System.out.println(Numeric.intPower(-1, 1000));
System.out.println("Expected: 1");
}
}
Write a JUnit
Make a JUnit test class for an earlier Homework Programming Exercise, such as P5.5
