Recursion
<< Sorting | HomeworkTrailIndex | Elevens Lab >>
Recursion
Demo 0: Factorial
If there are 6 people in a race where there is no ties, how many outcomes can there be? 6 possible can be first, leaving 5 people who could be in second, 4 people who could be third, 3 people who could come in fourth, 2 remain who could be second to last, and the remaining person would be last. In math we write 6! which means 6*5*4*3*2*1.
public class Factorial
{
public static void main (String[] args)
{
System.out.println("6! = "+factorial(6));
}
public static int factorial(int x){
// recursive code here
}
}
Recursive means that code calls itself. Like a loop, there is a danger of it never stopping (infinite recursion). In our code we see if we should end, in this case if x== 1, otherwise we return a call return factorial(x-1);
Demo 1: Triangle Numbers
We begin this chapter with a very simple example that demonstrates the power of thinking recursively. In this example, we will look at triangle shapes such as the ones from Section 6.3. We'd like to compute the area of a triangle of width n, assuming that each [] square has area 1. This value is sometimes called the nth triangle number. For example, as you can tell from looking at
[] [][] [][][]
the third triangle number is 6.
public class Triangle
{
public Triangle(int aWidth)
{
width = awidth;
}
public int getArea()
{
//your code here
}
private int width;
}
Now you Try:
Write a method that recursively make a String that counts down from any positive integer
public class RecursiveCountDownTester
{
public static void main(String[] args)
{
System.out.println("Countdown Tester from 10:");
System.out.println(countDown(10) );
}
}
Demo 2:Permutations
We will now turn to a more complex example of recursion that would be difficult to program with a simple loop. We will design a class that lists all permutations of a string. A permutation is simply a rearrangement of the letters. For example, the string “eat” has six permutations (including the original string itself):
"eat" "eta" "aet" "ate" "tea" "tae"
As in the preceding section, we will define a class that is in charge of computing the answer. In this case, the answer is not a single number but a collection of permuted strings. Here is our class:
PermutationGenerator.java
import java.util.*;
public class PermutationGenerator
{
private String word;
public PermutationGenerator(String aWord)
{
word=aWord;
}
ArrayList<String> getPermutations()
{
ArrayList<String> result=new ArrayList<String>();
if (word.length()==1)
{
result.add(word);
return result;
}
// otherwise make another permutation generator with a substring
// complete this with code on page 595 of the Horstman text
}
}
Here is the test program that prints out all permutations of the string “eat”:
PermutationGeneratorDemo.java
import java.util.ArrayList;
/**
This program demonstrates the permutation generator.
*/
public class PermutationGeneratorDemo
{
public static void main(String[] args)
{
PermutationGenerator generator
= new PermutationGenerator(“eat”);
ArrayList<String> permutations = generator.getPermutations();
for (String s : permutations)
{
System.out.println(s);
}
}
}
Demo3: Palindromes
Consider the palindrome "MOM" or "Do geese see God" -- they are the same if you spell them backwards. It is a bit inefficient to construct new Sentence objects in every step. Now consider the following change in the problem. Rather than testing whether the entire sentence is a palindrome, let's check whether a substring is a palindrome:
public class Sentence
{
private String text;
/**
Constructs a sentence.
@param aText a string containing all characters of the sentence
*/
public Sentence(String aText)
{
text = aText;
}
public String toString()
{
return text;
}
/**
Tests whether this sentence is a palindrome.
@return true if this sentence is a palindrome, false otherwise
*/
public boolean isPalindrome()
{
return isPalindrome(0, text.length() - 1);
}
/**
Tests whether a substring of the sentence is a palindrome.
@param start the index of the first character of the substring
@param end the index of the last character of the substring
@return true if the substring is a palindrome
*/
public boolean isPalindrome(int start, int end)
{
// Separate case for substrings of length 0 and 1.
if (start >= end) return true;
// Get first and last characters, converted to lowercase.
char first = Character.toLowerCase(text.charAt(start));
char last = Character.toLowerCase(text.charAt(end));
if (Character.isLetter(first) && Character.isLetter(last))
{
if (first == last)
{
// Test substring that doesn't contain the matching letters.
return isPalindrome(start + 1, end - 1);
}
else
return false;
}
else if (!Character.isLetter(last))
{
// Test substring that doesn't contain the last character.
return isPalindrome(start, end - 1);
}
else
{
// Test substring that doesn't contain the first character.
return isPalindrome(start + 1, end);
}
}
}
You should still supply a method to solve the whole problem—the user of your method shouldn't have to know about the trick with the substring positions. Simply call the helper method with positions that test the entire string:
public boolean isPalindrome()
{
return isPalindrome(0, text.length() - 1);
}
Note that this call is not a recursive method. The isPalindrome() method calls the helper method isPalindrome(int, int). In this example, we use overloading to define two methods with the same name. The isPalindrome method without parameters is the method that we expect the public to use. The second method, with two int parameters, is the recursive helper method. If you prefer, you can avoid overloaded methods by choosing a different name for the helper method, such as substringIsPalindrome.
Use the technique of recursive helper methods whenever it is easier to solve a recursive problem that is slightly different from the original problem.
Demo4: Fibonacci Sequence
Consider the Fibonacci sequence introduced in Exercise P6.4: a sequence of numbers defined by the equation
{⚠ $f_1=1$}
{⚠ $f_2=1$}
{⚠ $f_n=f_{n-2}+f_{n-1}$}
That is, each value of the sequence is the sum of the two preceding values. The first ten terms of the sequence are
{⚠ $ 1, 1, 2, 3, 5, 8, 13, 21, 34, 55$}
It is easy to extend this sequence indefinitely. Just keep appending the sum of the last two values of the sequence. For example, the next entry is 34 + 55 = 89.
We would like to write a function that computes {⚠ $f_n$} for any value of {⚠ $n$}. Let us translate the definition directly into a recursive method:
RecursiveFib.java
import java.util.Scanner;
/**
This program computes Fibonacci numbers using a recursive
method.
*/
public class RecursiveFib
{
public static void main(String[] args)
{
Scanner in = new Scanner(System.in);
System.out.print(“Enter n: ”);
int n = in.nextInt();
for (int i = 1; i <= n; i++)
{
long f = fib(i);
System.out.println(“fib(“ + i + ”) = ” + f);
}
}
/**
Computes a Fibonacci number.
@param n an integer
@return the nth Fibonacci number
*/
public static long fib(int n)
{
if (n <= 2) return 1;
else return fib(n - 1) + fib(n - 2);
}
}
This shows the call tree for computing fib(6):
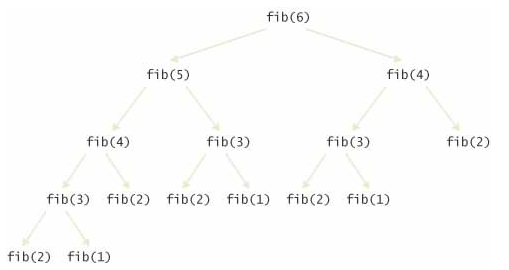
Now it is becoming apparent why the method takes so long. It is computing the same values over and over. For example, the computation of fib(6) calls fib(4) twice and fib(3) three times. That is very different from the computation we would do with pencil and paper. There we would just write down the values as they were computed and add up the last two to get the next one until we reached the desired entry; no sequence value would ever be computed twice. This is much more efficient:
LoopFib.java
import java.util.Scanner;
/**
This program computes Fibonacci numbers using an iterative method.
*/
public class LoopFib
{
public static void main(String[] args)
{
Scanner in = new Scanner(System.in);
System.out.print(“Enter n: ”);
int n = in.nextInt();
for (int i = 1; i <= n; i++)
{
long f = fib(i);
System.out.println(“fib(“ + i + ”) = ” + f);
}
}
/**
Computes a Fibonacci number.
@param n an integer
@return the nth Fibonacci number
*/
public static long fib(int n)
{
if (n <= 2) return 1;
long fold = 1;
long fold2 = 1;
long fnew = 1;
for (int i = 3; i <= n; i++)
{
fnew = fold + fold2;
fold2 = fold;
fold = fnew;
}
return fnew;
}
}
Demo 5: Sierpinski Gasket
import java.awt.*;
import java.applet.*;
public class SierpinskiGasket extends Applet {
public void paint (Graphics g) {
// draw black background square
g.setColor(Color.BLACK);
g.fillRect(0, 0, getWidth(), getHeight());
drawGasket(g, 0, 0, Math.min(getHeight(), getWidth()));
}
public void drawGasket(Graphics g, int x, int y, int side) {
// draw single white square in middle
int sub = side / 3; // length of sub-squares
g.setColor(Color.WHITE);
g.fillRect(x + sub, y + sub, sub - 1, sub - 1);
if(sub >= 3) {
// now draw eight sub-gaskets around the white square
drawGasket(g, x,y, sub);
drawGasket(g, x + sub,y, sub);
drawGasket(g, x + 2 * sub, y, sub);
drawGasket(g, x,y + sub, sub);
drawGasket(g, x + 2 * sub, y + sub, sub);
drawGasket(g, x,y + 2 * sub, sub);
drawGasket(g, x + sub,y + 2 * sub, sub);
drawGasket(g, x + 2 * sub, y + 2 * sub, sub);
}
}
}
Demo 6: TreeFractal
import java.awt.*;
import java.applet.*;
public class TreeFractal extends Applet
{
public void paint (Graphics g)
{
drawTree(g, getWidth()/2.0, getHeight()*.95, getHeight()/4.0, Math.PI/2.0);
}
public void drawTree(Graphics g, double x, double y, double len, double angle)
{
if(len >2){
double nextX= x + len* Math.cos(angle);
double nextY= y - len* Math.sin(angle);
g.setColor(Color.BLUE);
g.drawLine((int)Math.round(x), (int)Math.round(y),
(int)Math.round(nextX), (int)Math.round(nextY) );
drawTree(g, nextX, nextY, len * 0.75, angle + Math.PI/6.0);
drawTree(g, nextX, nextY, len * 0.66, angle - 5.0*Math.PI/18.0);
}
}
}
Just for fun, try this randColor() method, which favors browns and greens...
public Color randColor(){
int r=32+(int)(Math.random()*128);
int g=64+(int)(Math.random()*128);
int b=16+(int)(Math.random()*64);
return new Color(r,g,b);
}
Demo 7:Recursion without parameters or return
/**
* This demo shows that recursion can be done without a parameter
*
*/
public class Phrase
{
// instance variables - replace the example below with your own
private String phrase;
/**
* Constructor for objects of class Power Number
*/
public Phrase(String p)
{
// initialise instance variables
phrase = p;
}
/**
* This shows that you can have recursion even without parameters
* or returning anything
*/
public void reverse(){
if (phrase.indexOf(" ") <0) return;
String firstWord=getFirstWord();
Phrase shorterPhrase = new Phrase(getAllButTheFirstWord() );
shorterPhrase.reverse();
phrase=shorterPhrase.getPhrase()+" "+firstWord;
}
public String getPhrase()
{
return phrase;
}
public String getFirstWord()
{
int spaceLoc=phrase.indexOf(" ");
if (spaceLoc==-1)
return phrase;
return phrase.substring(0, spaceLoc);
}
public String getAllButTheFirstWord()
{
return phrase.substring(phrase.indexOf(" ")+1);
}
public String toString()
{
return phrase;
}
}
public class PhraseTester
{
// instance variables - replace the example below with your own
public static void main(String[] args)
{
Phrase p=new Phrase("Word Order is Important");
System.out.println(p);
p.reverse();
System.out.println(p);
}
}
Demo 8:EverGrowingTree
import java.awt.*;
import java.awt.event.*;
import java.applet.*;
/**
* Class EverGrowingTree - recursion demonstration
*
* @author Chris Thiel, OFMCap
* @version 13 Jan 2012
*/
public class EverGrowingTree extends Applet implements ActionListener
{
Button redrawButton;
int i=0;
public void init()
{
redrawButton= new Button("Redraw");
redrawButton.addActionListener(this);
add(redrawButton);
}
public void paint(Graphics g)
{
// simple text displayed on applet
g.setColor(Color.white);
g.fillRect(0, 0, getWidth(), getHeight());
drawTree(g, getWidth()/2, getHeight() );
}
public void drawTree(Graphics g, int w, int h)
{
g.setColor(Color.black);
g.drawLine(w,h, w, h-30);
g.drawLine(w,h-30, w-20, h-50);
g.drawLine(w,h-30, w+20, h-50);
if (Math.random()<.5)
drawTree(g, w-20, h-50);
if (Math.random()<.5)
drawTree(g, w+20, h-50);
}
public void actionPerformed(ActionEvent e)
{
repaint();
}
}
Demo 9: Maze Maker
Review Exercises
R13.8 Write a recursive definition of {⚠ $n! = 1 \times 2 \times … × n$}, similar to the recursive definition of the Fibonacci numbers
For those who love recursive graphics, here is a link to a great set of exercises from Dr. David Eck at Hobart and William Smith Colleges using Turtle Graphics . Start with making a project that has the TurtlePanel class and the TurtleGraphics class, then try the Koch Snowflake.
Programming Exercises
For 8 points do one of these four. For 9 points do two. For 10 do three. For 11 out of 10 do all four:
P13.1. Write a recursive method void reverse() that reverses a sentence. For example, if the text is "Hello!" after the reverse it becomes “!olleH”. Implement a recursive solution by removing the first character, reversing a sentence consisting of the remaining text, and combining the two.
Hint: since the reverse() method has no parameter, you will need to make a new Sentence that has the first letter stripped off, and then call the reverse() method on this new instance! That way you don't need a reverse(String s) that returns a String!
public class SentenceTester_13_1
{
public static void main(String[] args)
{
Sentence greeting = new Sentence("Hello!");
greeting.reverse();
System.out.println(greeting);
System.out.println("Expected \"!olleH\" ");
greeting.reverse();
System.out.println(greeting);
System.out.println("Expected \"Hello\" ");
}
}
Sentence.java for 13.1 and/or 13.4
public class Sentence
{
private String text;
/**
Constructs a sentence.
@param aText a string containing all characters of the sentence
*/
public Sentence(String aText)
{
text = aText;
}
public String toString()
{
return text;
}
/**
* 13.1 reverse the order of the text
*/
public void reverse()
{
// your code here
}
/**
* 13.4 use recursion to see if t is in text
*/
public boolean find(String t)
{
// your code here
return false;
}
}
P13.4 Use recursion to implement a method boolean find(String t) that tests whether a string is contained in a sentence. Hint 1: Use the String method startsWith(String s)
/**
A tester class for Sentence.
*/
public class SentenceTester_13_4
{
public static void main(String[] args)
{
Sentence s = new Sentence("Mississippi!");
boolean b = s.find("sip");
System.out.println(b);
System.out.println("Expected: true");
b = s.find("tip");
System.out.println(b);
System.out.println("Expected: false");
}
}
Hint2: If the text starts with the string you want to match, then you are done. If not, consider the sentence that you obtain by removing the first character. You can make a new instance of Sentence which is all but the first letter.
Hint 3: If the length of the string you are looking for is longer than the sentence, you know it is not there.
P13.7. Using recursion, compute the sum of all values in an array.
public class DataSet
{
private int[] values;
private int first;
private int last;
public DataSet(int[] values, int first, int last) { . . . }
public int getSum() { . . . }
}
/**
A tester class for the recursive sum.
*/
public class DataSetTester_13_7
{
public static void main(String[] args)
{
final int LENGTH = 10;
int[] values = new int[LENGTH];
for (int i = 0; i < values.length; i++)
{
values[i] = i - 5;
}
DataSet d1 = new DataSet(values, 0, 9);
System.out.println("Sum: " + d1.getSum());
System.out.println("Expected: -5");
DataSet d2 = new DataSet(values, 4, 8);
System.out.println("Sum: " + d2.getSum());
System.out.println("Expected: 5");
DataSet d3 = new DataSet(values, 2, 7);
System.out.println("Sum: " + d3.getSum());
System.out.println("Expected: -3");
}
}
P13.16 The recursive computation of Fibonacci numbers can be speeded up significantly by keeping track of the values that have already been computed. Provide an implementation of the fib method that uses this strategy. Whenever you return a new value, also store it in an auxiliary array. However, before embarking on a computation, consult the array to find whether the result has already been computed. Compare the running time of your improved implementation with that of the original recursive implementation and the loop implementation.
Use the following class as your tester class:
public class FastFibComputerTester
{
public static void main(String[] args)
{
FastFibComputer ffc = new FastFibComputer();
System.out.println(ffc.fib(50));
System.out.println("Expected: 12586269025");
System.out.println(ffc.fib(90));
System.out.println("Expected: 2880067194370816120");
}
}
Hint 1: Make an ArrayList<Long> of known values, and add a null to position 0 so that the index matches the fibonacci number.
Hint 2: Having wacky results in your ArrayList? When you want to add fibo number n, make sure there are n elements in the list (filling it with nulls), then use set rather than add to set the nth element to your fibo number.
