<< Picture Lab Activity 5 | Picture Lab | Picture Lab Activity 7 >>

Mirroring pictures

Video

Car designers at General Motors Research Labs only sculpt half of a car out of clay and then use a vertical mirror to reflect that half to see the whole car. What if we want to see what a picture would look like if we placed a mirror on a vertical line in the center of the width of the picture to reflect the left side.

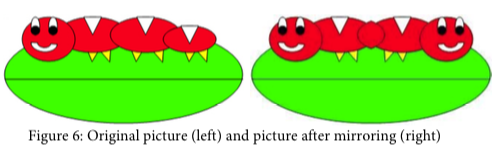
How can we write a method to mirror a picture in this way? One way to figure out the algorithm, which is a description of the steps for solving a problem, is to try it on smaller and simpler data. Figure 7 shows the result of mirroring a two-dimensional array of numbers from left to right vertically.

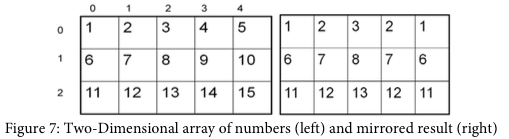
Can you figure out the algorithm for this process? Test your algorithm on different sizes of two- dimensional arrays of integers. Will it work for 2D arrays with an odd number of columns? Will it work for 2D arrays with an even number of columns?

public class TestWithInts
{

    public static void main(String[] args)
    {
       int[][] arr = {{1,2,3,4,5},{6,7,8,9,10},{11,12,13,14,15}};
       print(arr);
       //your code here
    }
    public static void print(int[][] a)
    {
        for (int r=0; r<a.length; r++){
           for(int c=0; c<a[0].length; c++)
               System.out.print(a[r][c]+" ");
           System.out.println();
        }      
    }
}

One algorithm is to loop through all the rows and half the columns. You need to get a pixel from the left side of the picture and a pixel from the right side of the picture, which is the same distance from the right end as the left pixel is from the left end. Set the color of the right pixel to the color of the left pixel. The column number at the right end is the number of columns, also known as the width, minus one. So assuming there are at least 3 pixels in a row, the first left pixel will be at row=0, col=0 and the first right pixel will be at row=0, col=width-1. The second left pixel will be at row=0, col=1 and the corresponding right pixel will be at row=0, col=width-1-1. The third left pixel will be at row=0, col=2 and its right pixel will be at row=0, col=width-1-2. Each time the left pixel is at (current row value, current column value), the corresponding right pixel is at (current row value, width - 1 - (current column value)).

The following method implements this algorithm. Note that, because the method is not looping through all the pixels, it cannot use a nested for-each loop.

public void mirrorVertical()
{ 
    Pixel[][] pixels = this.getPixels2D();
    Pixel leftPixel = null;
    Pixel rightPixel = null;
    int width = pixels[0].length;
    for (int row = 0; row < pixels.length; row++)
    { 
       for (int col = 0; col < width / 2; col++)
       { 
          leftPixel = pixels[row][col];
          rightPixel = pixels[row][width – 1 - col];
          rightPixel.setColor(leftPixel.getColor());
        } 
     } 
} 

You can test this with the testMirrorVertical method in PictureTester.

Exercises

1. Write the method mirrorVerticalRightToLeft that mirrors a picture around a mirror placed vertically from right to left. Hint: you can copy the body of mirrorVertical and only change one line in the body of the method to accomplish this. Write a class (static) test method called testMirrorVerticalRightToLeft in PictureTester to test this new method and call it in the main method.
2. Write the method mirrorHorizontal that mirrors a picture around a mirror placed horizontally at the middle of the height of the picture. Mirror from top to bottom as shown in the pictures below (Figure 8). Write a class (static) test method in PictureTester to test this new method and call it in the main method.
3. Write the method mirrorHorizontalBotToTop that mirrors the picture around a mirror placed horizontally from bottom to top. Hint: you can copy the body of mirrorHorizontal and only change one line to accomplish this. Write a class (static) test method in PictureTester to test this new method and call it in the main method.
4. Challenge — Work in groups to figure out the algorithm for the method mirrorDiagonal that mirrors just a square part of the picture from bottom left to top right around a mirror placed on the diagonal line (the diagonal line is the one where the row index equals the column index). This will copy the triangular area to the left and below the diagonal line as shown below. This is like folding a square piece of paper from the bottom left to the top right, painting just the bottom left triangle and then (while the paint is still wet) folding the paper up to the top right again. The paint would be copied from the bottom left to the top right as shown in the pictures below (Figure 9). Write a class (static) test method in PictureTester to test this new method and call it in the main method.